Els teus somnis i la teoria de la probabilitat

Fa uns mesos hi va haver molta revolada amb l’anunci televisiu del sorteig de la Loteria de Nadal, sovint denominat La grossa. A part del dubtós gust del director de l’anunci i de la controvertida actuació dels seus protagonistes, una de les frases amb les quals s’anima al públic a comprar loteria és: «posa els teus somnis a jugar». Aquesta frase donaria per escriure una tesi doctoral de Psicologia i una altra de Sociologia: com s’intenta relacionar aquest sorteig amb la felicitat de la gent, i quin efecte té sobre la població la monòtona repetició, any rere any, de connexions amb les administracions de loteria que han estat agraciades. Gent contenta, feliç, banyada amb cava, que comenta entusiasmada que, amb el premi, podran «tapar forats» o «fer el viatge de la seva vida». Aquest és el concepte de «somni fet realitat» amb el qual es pretén enganxar els potencials compradors de loteria.

Aquest sorteig tan especial té lloc una vegada a l’any, però els jocs d’atzar i les apostes tenen un paper destacat, i creixent, en l’economia. A més, l’auge de les noves tecnologies i l’accés a internet des d’ordinadors, mòbils i altres dispositius han posat a la disposició del públic una àmplia oferta de «productes i serveis de joc», per anomenar-ho d’alguna manera. Consegüentment, això comporta un gran creixement en aquest sector, on cada vegada més empreses competeixen per fer-se un lloc. Prenent com a exemple el camp de les apostes esportives, fins a fa relativament poc una empresa pública (Loteries i Apostes de l’Estat) tenia el monopoli mitjançant la històrica travessa. Avui dia, diverses empreses privades (Bet and Win, Miapuesta.es, etc.) lluiten per copar el sector, el qual es nodreix d’una demanda caracteritzada per la necessitat del públic d’ apostar.

Algú va dir una vegada que «la loteria és un impost que paguen els que no saben matemàtiques». És cert que no anava desencaminat, ja que la loteria va néixer com un mecanisme públic de recaptació, i avui dia, encara que ha canviat molt el sistema, segueix la mateixa lògica. És a dir, el que organitza un sorteig mai no perd diners i sempre es recapta més del que es reparteix en premis, ja sigui Loteries i Apostes de l’Estat, una empresa d’apostes en línia o un casino. Llavors cal preguntar-se: fins a quin punt és racional el fet d’apostar o comprar bitllets de loteria? En aquest article es pretén analitzar aquesta qüestió des d’un punt de vista matemàtic, introduint alguns conceptes fonamentals de la teoria de la probabilitat. A més, analitzarem detalladament el mecanisme del sorteig de la Loteria de Nadal, per comprovar quines són les probabilitats reals d’obtenir algun premi i de no obtenir-ne cap, a més d’analitzar a llarg termini les probabilitats reals de fes-se ric.

Dos conceptes fonamentals en estadística són els de variable aleatòria (X), i el de la seva esperança matemàtica (també coneguda com a valor esperat), definida com E(X). Per explicar-los, suposem que ens plantegen un joc molt senzill, que consisteix a llançar una moneda a l’aire. Si surt cara, ens paguen un premi, i si surt creu, no ens en paguen res. Ara bé, per participar en aquest joc, que consisteix en un únic llançament, hem de pagar un preu. Suposem que el premi és de 100 €. La pregunta és: quan ens interessarà jugar i quan no? El primer que voldrem saber és quin és el ventall de premis possible en aquest joc, que són bàsicament dos: o bé 100 € si surt cara, o bé res (0 €) si surt creu. Aquestes dues xifres formen el que es denomina espai mostral, això és, el conjunt de tots els possibles resultats individuals d’un experiment aleatori (el llançament de la moneda a l’aire). Matemàticament, l’espai mostral es defineix tal com expressa l’equació de la figura 1.

 

Figura 1.

Amb això, ja podem definir aquests conceptes. D’una banda, una variable aleatòria és una manera de quantificar (això és, expressar amb nombres) els possibles resultats d’un procés aleatori, com pot ser el llançament de la moneda. En el nostre exemple, a la variable aleatòria X la podem anomenar premi resultant de l’experiment, i formalment l’expressaríem segons l’equació de la figura 2.

 

Figura 2.

El següent pas és saber les probabilitats que surti cara i que surti creu. Suposant que la moneda sigui normal i no estigui trucada, les probabilitats són idèntiques: 50% que surti cara i 50% que surti creu. En estadística s’expressen les probabilitats en tant per u, de manera que definirem pc = 0,5 a la probabilitat que surti cara, i px = 0,5 a la probabilitat que surti creu.

Amb aquests elements, ja podem definir i calcular l’esperança matemàtica d’aquest experiment aleatori. Aquesta serà bàsicament la suma dels possibles resultats de l’experiment ponderats per les seves respectives probabilitats. Formalment es calcula tal com expressa la figura 3.

Figura 3.

Com hem d’interpretar aquest valor? Una manera de veure-ho és la següent: imaginem-nos que repetim el joc moltes vegades, diguem que n vegades. Per les lleis de la probabilitat, com més vegades ho repetim, el nombre de cares i de creus obtingudes es tendirà a igualar, ja que tenen la mateixa probabilitat de sortir. Així que just la meitat de les vegades (n/2) guanyarem el premi, i l’altra meitat de les vegades (n/2) no guanyarem res. Si llavors dividim el premi total rebut entre el nombre d’intents, obtindrem el valor esperat del joc mitjançant l’equació de la figura 4.

 

Figura 4.

Quan valdrà la pena jugar? Suposem que el joc és diari i que hi ha una persona que hi participa cada dia. Llavors, a llarg termini, si el preu del bitllet és menor de 50, la persona guanyarà diners; si val més de 50, perdrà diners; i si val exactament 50, guanyarà igual que perdrà, amb la qual cosa serà indiferent que jugui o no. Per això, davant la pregunta: quant pagaries per jugar cada vegada? La resposta racional és que, com a màxim, pagaré el valor esperat del joc E(X). Però, com s’ha comentat anteriorment, la decisió de comprar loteria i apostar no es caracteritza per seguir un criteri racional, precisament.

El format del sorteig de Nadal de Loteries i Apostes de l’Estat no és molt diferent de l’exemple que acabem de veure. L’única diferència, essencialment, és que hi ha més tipus de boles, més premis i més probabilitats. L’estructura del sorteig és la següent: hi ha un total de n = 100.000 números, des del 0 fins al 99.999. Per apostar per un d’ells, es pot adquirir una sèrie per un preu de 200 €, o un dècim d’aquesta sèrie, el qual costa una desena part d’una sèrie, això és, 20 €. A més, es pot adquirir una sèrie i dividir-la en participacions, les quals es venen a un preu menor.

El dia del sorteig es disposen dos bombos. En el més gran s’inclouen tots els n = 100.000 números, cadascun en una bola. En el bombo menor s’inclouen les boles amb els premis. Llavors, es va extraient una bola de cada bombo i aquestes s’associen, això és, a cada premi li correspon un número. La taula 1 mostra el tipus de premi, el número de boles associades (això és, la freqüència absoluta), la seva probabilitat (que és la freqüència dividida entre 100.000) i l’import del premi.

Taula 1. Taula de freqüències dels premis del Sorteig de Nadal

Classe de premi	k	Núm. de boles (freqüència)	Probabilitat (pk)	Import (Xk)
Primer premi	1	1	0,00001	4.000.000
Segon premi	2	1	0,00001	1.250.000
Tercer premi	3	1	0,00001	500.000
Quart premi	4	2	0,00002	200.000
Cinquè premi	5	8	0,00008	60.000
Pedrea	6	1.794	0,01794	1.000
Números anterior y posterior al 1r premi	7	2	0,00002	20.000
Números anterior y posterior al 2n premi	8	2	0,00002	12.500
Números anterior y posterior al 3r premi	9	2	0,00002	9.600
Centenes dels premis 1r, 2n i 3r	10	297	0,00297	1.000
Centenes dels premis 4t i 5è	11	198	0,00198	1.000
Dues últimes xifres dels premis 1r, 2n i 3r	12	2.547	0,02547	1.000
Reintegrament	13	8.499	0,08499	200
Res	14	86.646	0,86646	0

Font: Loteries i Apostes de l’Estat

 

En total, el nombre de premis repartit (sense incloure el reintegrament) s’obté sumant la tercera columna menys les dues últimes xifres. El resultat és de 4.855 números agraciats. Si els comparem amb el total de premis a concurs, obtenim que només un 4,85 % dels bitllets posats a la venda reben un premi, o vist d’una altra manera, el 95 % dels bitllets rep o bé el reintegrament o res. Vist amb la perspectiva que ens dóna l’estadística, una persona que jugués a un número cada any, obtindria aproximadament un premi cada 20 anys (5/100 = 1/20).

Per calcular el valor esperat E(X) d’aquest joc, hem de multiplicar les probabilitats (pk) pels possibles premis (Xk) i després sumar el conjunt, tal com mostra la fórmula de la figura 5.

 

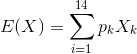
Figura 5.

Això equival a multiplicar element a element les dues columnes de la dreta de la taula 1 i sumar la columna resultant. El resultat d’aquesta operació és E(X) = 132,5. Com podem interpretar aquest resultat? Aquesta xifra s’ha obtingut considerant X com a premis per sèrie, el preu de la qual és 200 €. Seria més intuïtiu calcular el valor esperat del joc per euro jugat, la qual cosa s’obté dividint E(X) entre 200. La xifra que obtenim és 0,6625, la qual cosa correspon, aproximadament, a dos terços (2/3). Aquest resultat és més fàcil d’interpretar: per cada euro apostat en aquest sorteig, el valor esperat és de 0,66 euros. Això significa que, amb el temps, si apostéssim a molts números durant molts anys, a llarg termini el total acumulat de premis rebuts tendiria a ser només dues terceres parts de l’import total gastat en loteria.

Per analitzar aquest resultat gràficament, realitzarem una simulació, que consisteix a generar valors aleatoris i comprovar els paràmetres estimats del joc quan es juga repetides vegades. A més, volem analitzar el resultat d’apostar tot a un sol número o a diversos números. Per fer la simulació, plantejarem tres escenaris, en cadascun dels quals el jugador divideix cada euro apostat entre k = 1, 10, 20 números. Per a cada escenari repetim el joc n = 50.000 vegades. Per a cadascuna d’aquestes repeticions i valor de k , extraurem de la distribució de premis k números a l’atzar, els quals poden estar premiats o no. Al final, l’objectiu d’aquesta simulació és veure, per al número de repetició q més gran o igual CARACTER n, quin valor pren el quocient entre tots els premis guanyats i el desemborsament total fins al moment. El resultat es pot veure en la figura 6, en la qual cada corba correspon a un valor de k (números apostats).

 

 

 

 

 

 

 

 

 

Figura 6. Tendència a llarg termini del quocient entre ingressos i despeses acumulades

 

En la figura 6, la línia horitzontal discontínua és el valor esperat 0,6625. En les tres corbes representades es poden observar tres fets interessants. 

a) El valor de cada corba (el quocient entre ingressos i despeses acumulades), especialment per als valoris k = 10 i k= 20, tendeix al valor asimptòtic E(X) = 0,6635, tal com s’ha calculat anteriorment.

b) En tots els casos, arribats a un nombre de repeticions, s’obté un premi major que eleva el valor de les corbes, puntualment fent que el quocient entre ingressos i despeses acumulades superi àmpliament el valor 1, el qual marca el llindar entre la diferència neta entre ingressos i despeses acumulades. No obstant això, a partir d’aquest període, el valor del quocient torna a decréixer i tendeix gradualment al valor asimptòtic E(X) = 0,6635.

c) A major nombre de números apostats (k), s’amplia la probabilitat de guanyar més premis, per això mateix, les corbes corresponents a k = 10 i k = 20 tenen més pics i variacions que la corba corresponent a k = 1.

Aquests tres punts es poden resumir en la següent conclusió: encara que a molt llarg termini el quocient entre ingressos i despeses acumulades tendeix a E(X) = 0,6635, la qual cosa indica que només es recuperen 2/3 parts dels diners invertits, sempre hi haurà un període en el qual s’aconsegueixi un premi major, de manera que durant molts períodes el quocient entre ingressos i despeses acumulades serà alt, però decreixent. Ara bé, existeix un problema: tractant-se d’un sorteig anual, aquest període de sort pot trigar a arribar centenars d’anys, i ningú viu tant temps, de moment, per poder explicar-ho.

En aquest article s’ha analitzat des d’un punt de vista estadístic i probabilístic el mecanisme i la interpretació dels jocs d’atzar consistents en l’extracció de boles d’una urna. Per a això, s’han introduït els conceptes de variable aleatòria, espai mostral, esperança matemàtica i valor esperat. Per il·lustrar aquests conceptes s’ha desenvolupat un senzill exemple, en el qual s’ha comparat el valor esperat del joc amb el que costa jugar. Aquests conceptes teòrics s’han aplicat, seguidament, a un exemple real: el sorteig de Nadal de Loteries i Apostes de l’Estat. Mitjançant l’anàlisi estadística dels diferents premis que reparteix i la seva probabilitat associada, s’ha arribat a la conclusió que el valor esperat del premi és aproximadament de dos terços. Això significa que, per cada euro que s’inverteix regularment, només es recuperen a llarg termini 0,66 €. Una simulació realitzada amb aquestes dades ha constatat gràficament aquest resultat, i ha mostrat també que el fet de repartir la despesa en el joc entre més números jugats augmenta la probabilitat d’ampliar el nombre de premis guanyats, encara que el valor asimptòtic segueixi sent de dos terços.

Quina conclusió es pot extreure de tot això? D’una banda, es pot afirmar que la decisió d’apostar en aquest tipus de jocs d’atzar no és racional, ja que probabilísticament, en la immensa majoria de casos, el resultat serà una pèrdua econòmica. Així, doncs, en la compra de bitllets de loteria, i en la participació en jocs d’atzar (així com en apostes esportives), intervenen molts altres factors que expliquen que aquests sectors estiguin a l’alça, com factors de caràcter psicològic i sociològic com la tradició, l’efecte de la publicitat i l’efecte addictiu que té el joc en algunes persones. A més, també existeix la percepció que apostar en loteria implica pagar un import relativament petit a canvi de la possibilitat d’obtenir un premi molt gran. Dues observacions desmunten aquesta percepció: (a) la possibilitat d’obtenir el premi gran és molt, molt, molt reduïda i, (b) en jugar a la loteria repetidament, a llarg termini l’import total destinat al joc deixa de ser petit.

LIVIANO SOLÍS, Daniel. Els teus somnis i la teoria de la probabilitat. Oikonomics [en línia]. Maig 2014, no. 1, pp. 106-111. ISSN: 2339-9546. DOI: https://doi.org/10.7238/o.n1.1410

---

ODS