Tus sueños y la teoría de la probabilidad

Hace unos meses hubo mucho revuelo con el anuncio televisivo del sorteo de la Lotería de Navidad, comúnmente denominado El gordo. A parte del dudoso gusto del director del anuncio y de la controvertida actuación de sus protagonistas, una de las frases con las que se anima al público a comprar lotería es «pon tus sueños a jugar». Dicha frase daría para escribir una tesis doctoral de Psicología y otra de Sociología: cómo se intenta relacionar este sorteo con la felicidad de la gente, y qué efecto tiene sobre la población la monótona repetición, año tras año, de conexiones con las administraciones de lotería que han sido agraciadas. Gente contenta, feliz, bañada con cava, que comenta entusiasmada que, con el premio, podrán «tapar agujeros» o «hacer el viaje de su vida». Ese es el concepto de «sueño hecho realidad» con el que se pretende enganchar a los potenciales compradores de lotería.

Este sorteo tan especial tiene lugar una vez al año, pero los juegos de azar y las apuestas tienen un papel destacado, y creciente, en la economía. Además, el auge de las nuevas tecnologías y el acceso a internet desde ordenadores, móviles y otros dispositivos han puesto a disposición del público una amplia oferta de «productos y servicios de juego», por llamarlo de alguna manera. Consiguientemente, esto conlleva un gran crecimiento en este sector, donde cada vez más empresas compiten para hacerse un hueco. Tomando como ejemplo el campo de las apuestas deportivas, hasta hace relativamente poco una empresa pública (Loterías y Apuestas del Estado) tenía el monopolio mediante la histórica quiniela. Hoy en día, varias empresas privadas (Bet and Win, Miapuesta.es, etc.) luchan por copar el sector, el cual se nutre de una demanda caracterizada por la necesidad del público de apostar.

Alguien dijo una vez que «la lotería es un impuesto que pagan los que no saben matemáticas». Cierto es que no iba desencaminado, ya que la lotería nació como un mecanismo público de recaudación, y hoy en día, aunque ha cambiado mucho el sistema, sigue la misma lógica. Es decir, el que organiza un sorteo nunca pierde dinero y siempre se recauda más de lo que se reparte en premios, ya sea Loterías y Apuestas del Estado, una empresa de apuestas en línea o un casino. Entonces cabe preguntarse: ¿hasta qué punto es racional el hecho de apostar o comprar boletos de lotería? En este artículo se pretende arrojar un poco de luz sobre este tema desde un punto de vista matemático, introduciendo algunos conceptos fundamentales de la teoría de la probabilidad. Además, analizaremos detalladamente el mecanismo del sorteo de la Lotería de Navidad, para comprobar cuáles son las probabilidades reales de obtener algún premio y de no obtener nada, además de analizar a largo plazo las probabilidades reales de hacerse rico.

Dos conceptos fundamentales en estadística son los de variable aleatoria (X), y el de su esperanza matemática (también conocida como valor esperado), definida como E(X). Para explicarlos, supongamos que nos plantean un juego muy sencillo, consistente en lanzar una moneda al aire. Si sale cara, nos pagan un premio, y si sale cruz, no nos pagan nada. Ahora bien, para participar en este juego, consistente en un único lanzamiento, hemos de pagar un precio. Supongamos que el premio es de 100 €. La pregunta es: ¿cuándo nos interesará jugar y cuándo no? Lo primero que querremos saber es cuál es el abanico de premios posible en este juego, que son básicamente dos: o bien 100 € si sale cara, o bien nada (0 €) si sale cruz. Estas dos cifras forman lo que se denomina espacio muestral, esto es, el conjunto de todos los posibles resultados individuales de un experimento aleatorio (el lanzamiento de la moneda al aire). Matemáticamente, el espacio muestral se define tal como expresa la ecuación de la figura 1.

Figura 1

Con esto, ya podemos definir estos conceptos. Por una parte, una variable aleatoria es una manera de cuantificar (esto es, expresar con números) los posibles resultados de un proceso aleatorio, como puede ser el lanzamiento de la moneda. En nuestro ejemplo, a la variable aleatoria X la podemos llamar premio resultante del experimento, y formalmente la expresaríamos según la ecuación de la figura 2.

 

Figura 2

El siguiente paso es saber las probabilidades de que salga cara y que salga cruz. Suponiendo que la moneda sea normal y no esté trucada, las probabilidades son idénticas: 50% de que salga cara y 50% de que salga cruz. En estadística se expresan las probabilidades en tanto por uno, de manera que definiremos pc = 0,5 a la probabilidad de que salga cara, y px = 0,5 a la probabilidad de que salga cruz.

Con estos elementos, ya podemos definir y calcular la esperanza matemática de este experimento aleatorio. Ésta será básicamente la suma de los posibles resultados del experimento ponderados por sus respectivas probabilidades. Formalmente se calcula tal como expresa la ecuación de la figura 3.

Figura 3

¿Cómo hemos de interpretar este valor? Una manera de verlo es la siguiente: imaginémonos que repetimos el juego muchas veces, digamos que n veces. Por las leyes de la probabilidad, cuantas más veces lo repitamos, el número de caras y de cruz obtenidos se tenderá a igualar, ya que tienen la misma probabilidad de salir. Así que justo la mitad de las veces (n/2) ganaremos el premio y la otra mitad de las veces (n/2) no ganaremos nada. Si entonces dividimos el premio total recibido entre el número de intentos, obtendremos el valor esperado del juego mediante la ecuación de la figura 4.

 

Figura 4

¿Cuándo valdrá la pena jugar? Supongamos que el juego es diario y que hay una persona que participa cada día. Entonces, a largo plazo, si el precio del billete es menor de 50, la persona ganará dinero; si vale más de 50, perderá dinero; y si vale exactamente 50, ganará igual que perderá, con lo cual será indiferente que juegue o no. Por eso, ante la pregunta: ¿cuánto pagarías por jugar cada vez? La respuesta racional es que, como máximo, pagaré el valor esperado del juego E(X). Pero, como se ha comentado anteriormente, la decisión de comprar lotería y apostar no se caracteriza por seguir un criterio racional, precisamente.

El formato del sorteo de Navidad de Loterías y Apuestas del Estado no es muy diferente del ejemplo que acabamos de ver. La única diferencia, esencialmente, es que hay más tipos de bolas, más premios y más probabilidades. La estructura del sorteo es la siguiente: Hay un total de n = 100.000 números, desde el 0 hasta el 99.999. Para apostar por uno de ellos, se puede adquirir una serie por un precio de 200 €, o un décimo de esa serie, el cual cuesta una décima parte que una serie, esto es, 20 €. Además, se puede adquirir una serie y dividirla en participaciones, las cuales se venden a un precio menor.

El día del sorteo se disponen dos bombos. En el mayor se incluyen todos los n = 100.000 números, cada uno en una bola. En el bombo menor se incluyen las bolas con los premios. Entonces, se va extrayendo una bola de cada bombo y éstas se asocian, esto es, a cada premio le corresponde un número. La tabla 1 muestra el tipo de premio, el número de bolas asociadas (esto es, la frecuencia absoluta), su probabilidad (que es la frecuencia dividida entre 100.000) y el importe del premio.

Tabla 1. Tabla de frecuencias de los premios del Sorteo de Navidad

Clase de premio	k	Nº de bolas (frecuencia)	Probabilidad (pk)	Importe (Xk)
Primer premio	1	1	0,00001	4.000.000
Segundo premio	2	1	0,00001	1.250.000
Tercer premio	3	1	0,00001	500.000
Cuarto premio	4	2	0,00002	200.000
Quinto premio	5	8	0,00008	60.000
Pedrea	6	1.794	0,01794	1.000
Números anterior y posterior al 1º premio	7	2	0,00002	20.000
Números anterior y posterior al 2º premio	8	2	0,00002	12.500
Números anterior y posterior al 3º premio	9	2	0,00002	9.600
Centenas de los premios 1º, 2º y 3º	10	297	0,00297	1.000
Centenas de los premios 4º y 5º	11	198	0,00198	1.000
Dos últimas cifras de los premios 1º, 2º y 3º	12	2.547	0,02547	1.000
Reintegro	13	8.499	0,08499	200
Nada	14	86.646	0,86646	0

Fuente: Loterías y Apuestas del Estado

 

En total, el número de premios repartido (sin incluir el reintegro) se obtiene sumando la tercera columna menos las dos últimas cifras. El resultado es de 4.855 números agraciados. Si los comparamos con el total de premios a concurso, obtenemos que sólo un 4,85 % de los boletos puestos a la venta reciben un premio, o visto de otra manera, el 95 % de los boletos recibe o el reintegro o nada. Visto con la perspectiva que nos da la estadística, una persona que jugara a un número cada año, obtendría aproximadamente un premio cada 20 años (5/100 = 1/20).

Para calcular el valor esperado E(X) de este juego, hemos de multiplicar las probabilidades (pk) por los posibles premios (Xk) y después sumar el conjunto, tal y como muestra la fórmula de la figura 5.

 

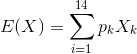
Figura 5

Esto equivale a multiplicar elemento a elemento las dos columnas de la derecha de la tabla 1 y sumar la columna resultante. El resultado de esta operación es E(X) = 132,5. ¿Cómo podemos interpretar este resultado? Esta cifra se ha obtenido considerando X como premios por serie, el precio de la cual es 200 €. Sería más intuitivo calcular el valor esperado del juego por euro jugado, lo cual se obtiene dividiendo E(X) entre 200. La cifra que obtenemos es 0,6625, lo cual corresponde, aproximadamente, a dos tercios (2/3). Este resultado es más fácil de interpretar: por cada euro apostado en este sorteo, el valor esperado es de 0,66 euros. Esto significa que, con el tiempo, si apostáramos a muchos números durante muchos años, a largo plazo el total acumulado de premios recibidos tendería a ser sólo dos terceras partes del importe total gastado en lotería.

Para analizar este resultado gráficamente, realizaremos una simulación, consistente en generar valores aleatorios y comprobar los parámetros estimados del juego cuando se juega repetidas veces. Además, queremos analizar el resultado de apostar todo a un solo número o a varios de estos. Para hacer la simulación, plantearemos tres escenarios, en cada uno de los cuales el apostante divide cada euro apostado entre k =1, 10, 20 números. Para cada escenario repetimos el juego n = 50.000 veces. Para cada una de estas repeticiones y valor de k, extraeremos de la distribución de premios k números al azar, los cuales pueden estar premiados o no. Al final, el objetivo de esta simulación es ver, para el número de repetición q ≤ n, qué valor toma el cociente entre todos los premios ganados y el desembolso total hasta el momento. El resultado se puede ver en la figura 6, en la cual cada curva corresponde a un valor de k (números apostados).

 

 

 

 

 

 

 

 

 

Figura 6. Tendencia a largo plazo del cociente entre ingresos y gastos acumulados

 

En la figura 6, la línea horizontal discontinua es el valor esperado 0,6625. En las tres curvas representadas se pueden observar tres hechos interesantes. 

a) El valor de cada curva (el cociente entre ingresos y gastos acumulados), especialmente para los valores k = 10 y k= 20, tiende al valor asintótico E(X) = 0,6635, tal y como se ha calculado anteriormente.

b) En todos los casos, llegado a un número de repeticiones, se obtiene un premio mayor que eleva el valor de las curvas, puntualmente haciendo que el cociente entre ingresos y gastos acumulados supere ampliamente el valor 1, el cual marca el umbral entre la diferencia neta entre ingresos y gastos acumulados. Sin embargo, a partir de ese periodo, el valor del cociente vuelve a decrecer y tiende gradualmente al valor asintótico E(X) = 0,6635.

c) A mayor número de números apostados (k), se amplía la probabilidad de ganar más premios, por eso mismo, las curvas correspondientes a k = 10 y k = 20 tienen más picos y variaciones que la curva correspondiente a k = 1. 

Estos tres puntos se pueden resumir en la siguiente conclusión: aunque a muy largo plazo el cociente entre ingresos y gastos acumulados tiende a E(X) = 0,6635, lo cual indica que sólo se recuperan 2/3 partes del dinero invertido, siempre habrá un periodo en el cual se consiga un premio mayor, de manera que durante muchos periodos el cociente entre ingresos y gastos acumulados será alto, pero decreciente. Ahora bien, existe un problema: tratándose de un sorteo anual, este periodo de suerte puede tardar en llegar cientos de años, y nadie vive tanto tiempo, de momento, para poder contarlo.

En este artículo se ha analizado desde un punto de vista estadístico y probabilístico el mecanismo y la interpretación de los juegos de azar consistentes en la extracción de bolas de una urna. Para ello, se han introducido los conceptos de variable aleatoria, espacio muestral, esperanza matemática y valor esperado. Para ilustrar estos conceptos se ha desarrollado un sencillo ejemplo, en el cual se ha comparado el valor esperado del juego con lo que cuesta jugar. Estos conceptos teóricos se han aplicado, seguidamente, a un ejemplo real: el Sorteo de Navidad de Loterías y Apuestas del Estado. Mediante el análisis estadístico de los diferentes premios que reparte y su probabilidad asociada, se ha llegado a la conclusión de que el valor esperado del premio es aproximadamente de dos tercios. Esto significa que, por cada euro que se invierte regularmente, sólo se recuperan a largo plazo 0,66 €. Una simulación realizada con estos datos ha constatado gráficamente este resultado, mostrando también que el hecho de repartir el gasto en el juego entre más números jugados aumenta la probabilidad de ampliar el número de premios ganados, aunque el valor asintótico siga siendo de dos tercios.

¿Qué conclusión se puede extraer de todo esto? Por una parte, se puede afirmar que la decisión de apostar en este tipo de juegos de azar no es racional, ya que probabilísticamente en la inmensa mayoría de casos el resultado será una pérdida económica. Así pues, en la compra de boletos de lotería y en la participación en juegos de azar (así como en apuestas deportivas), intervienen otros muchos factores que explican que estos sectores estén al alza,como factores de carácter psicológico y sociológico como la tradición, el efecto de la publicidad y el efecto adictivo que tiene el juego en algunas personas. Además, también existe la percepción de que apostar en lotería implica pagar un importe relativamente pequeño a cambio de la posibilidad de obtener un premio muy grande. Dos observaciones desmontan esta percepción: (a) la posibilidad de obtener el premio grande es muy, muy, muy reducida y, (b) al jugar a la lotería repetidamente, a largo plazo el importe total destinado al juego deja de ser pequeño.

LIVIANO SOLÍS, Daniel. Tus sueños y la teoría de la probabilidad. Oikonomics [en línea]. Mayo 2014, no. 1, pp. 106-111. ISSN: 2339-9546. DOI: https://doi.org/10.7238/o.n1.1410

---

ODS